Estimación de volúmenes maderables en plantaciones de Pinus patula en la Cooperativa Atahualpa Jerusalén Granja Porcón, Cajamarca

Estimation of timber volumes in Pinus patula plantations in the Atahualpa Jerusalem Farm Porcón Cooperative, Cajamarca

Fátima E. Marcelo-Bazán^1,a,*, Juan R. Baselly-Villanueva^1,b, Jim J. Villena-Velásquez^1,c

¹ Estación Experimental Agraria Baños del Inca, Instituto Nacional de Innovación Agraria (INIA). Cajamarca, Perú.

^a Ing., bk.fatimamarcelo@gmail.com, https://orcid.org/0000-0002-6340-3670

^b Ing., jrbaselly@gmail.com, https://orcid.org/0000-0001-7795-7925

^c Mg., jimjairo@hotmail.com, https://orcid.org/0000-0003-4958-3860

* Autor de Correspondencia: Tel. +51 986123238

http://dx.doi.org/10.25127/riagrop.20224.876

Resumen

En la región Cajamarca desde los años 70 se han desarrollado diversas investigaciones relacionadas a la introducción y adaptación de especies exóticas, siendo el Pinus patula una de ellas, lo cual motivó el establecimiento de grandes plantaciones o macizos forestales en la Cooperativa Agraria Atahualpa Jerusalén – Granja Porcón. La siguiente investigación tiene como finalidad principal estimar volúmenes maderables de una plantación forestal ubicada en Cerro Campanario de la sierra norte del país. Se instaló un conjunto de parcelas con un muestreo al azar y se ajustaron cuatro volúmenes matemáticos para la estimación volumétrica. Se determinó que los modelos  y , presentaron las mejores estimaciones con un coeficiente de correlación ( mínimo de 0.975 y un Error padrón residual () máximo de 0.636; además, se obtuvo que la plantación presentó un volumen total (VT)  y comercial (VC) de 718.4397 m³ha^-1 y 277.0618 m³ha^-1 respectivamente.

Palabras claves: Clases diamétricas; error de muestreo; inventario forestal; macizo forestal; modelos volumétricos.

Abstract

In the Cajamarca region since the 70s, various investigations related to the introduction and adaptation of exotic species have been carried out, being the Pinus patula one of them, which motivated the establishment of large plantations or forest massifs in the Cooperativa Agraria Atahualpa Jerusalen - Granja Porcón. The main purpose of the following research is to estimate timber volumes of a forest plantation located in Cerro Campanario in the northern highlands of the country. A set of plots was installed with a random sampling and four mathematical volumes were adjusted for the volumetric estimation. It was determined that the models  y , presented the best estimates with a correlation coefficient ( minimum of 0.975 and a maximum residual standard error () of 0.636; Furthermore, it was obtained that the plantation had a total volume (VT) and commercial volume (VC) of 718.4397 m3ha-1 and 277.0618 m³ha-1 respectively.

Keywords: Diameter classes; sampling error; forest inventory; forest massif; volumetric models.

1. INTRODUCCIÓN

La región de Cajamarca ubicada en los Andes del Norte del Perú, presenta condiciones climáticas favorables para las actividades agropecuarias y forestales que el resto de la sierra peruana, por este motivo a fines de los años 60 se ejecutaron actividades para fomentar el desarrollo forestal (Carton, 1996). Los primeros ensayos para introducir especies forestales en la región empezaron de manera sistemática a principios de 1976, en el marco del Proyecto Centro de Investigación y Capacitación Forestal (CICAFOR), la metodología usada tuvo 4 fases: eliminación, prueba, comprobación y plantación piloto (Picard y Villar 1986). En base a los resultados favorables adquiridos por el CICAFOR en la reforestación de las regiones Quechua Alta y Jalca en Cajamarca se decidió establecer un macizo forestal piloto, instalándose entre las campañas 1983 – 1989 una extensión de 3 572 ha, de las cuales el 62.5% era Pinus patula (Carton, 1996). Hasta el 2012 según las estadísticas oficiales en el Perú las plantaciones con fines de producción y protección suman más de 1 032 386 ha, y en su mayoría se tratan de plantaciones forestales de especies exóticas como el Eucalyptus globulus, Pinus radiata y Pinus patula (FAO, 2016).

El Pinus patula es una especie conífera nativa de regiones subtropicales de México, distribuyéndose desde el norte del estado de Hidalgo hasta Cofre de Perote, entre los 1500 y 3100 metros de en altitud (Dvorak et al., 2000). Por su rápido crecimiento ha sido extensamente utilizado en varios países, en Sudamérica se han establecido plantaciones en Argentina, Brasil, Venezuela, Colombia, Ecuador y Perú (Ospina et al., 2011). Su madera es suave de 0.46 a 0.48 g/cm³, siendo empleada en estructuras que no requieren grandes resistencias (Del Pozo 1996). En la región Cajamarca se ha adaptado muy bien en zonas altas, entre los 2700 y 3400 msnm con temperaturas promedios de 8 a 12°C y en suelos de origen volcánico; soportando heladas y el ataque de Dothistroma pini (Asociación Civil para la Investigación y Desarrollo Forestal, 1996).

Para una adecuada aplicación de las técnicas de manejo silvicultural se debe contar con una buena información volumétrica del bosque, las funciones o modelos de volumen son ecuaciones matemáticas que cuando son ajustadas a una muestra de la población de interés, pueden ser posteriormente utilizadas en las estimaciones de volúmenes de árboles en pie (Higuera, 1994). El volumen de un árbol está en función de variables o mediciones fáciles de obtener como el diámetro a la altura del pecho (DAP) y altura del árbol (Cailliez, 1980). Dependiendo de las variables independientes usadas para el ajuste, existen tres tipos de modelos volumétricos: los modelos volumétricos locales que requieren sólo del DAP, los modelos de volumen general requieren del DAP y altura de planta; y finalmente los modelos volumétricos con clase de forma, los cuales además los cuales adicionan el factor de forma para su construcción (Campos, 1970).

La siguiente investigación se desarrolló en un macizo forestal de Pinus patula ubicada en la Cooperativa Agraria Atahualpa Jerusalén, teniendo como finalidad principal determinar volúmenes maderables, el error de muestreo y el mejor modelo que estime los volúmenes de los árboles en pie.

2. MATERIALES Y MÉTODOS

2.1. Lugar de estudio

La presente investigación se desarrolló en la plantación forestal de Pinus patula instalada en Cerro Campanario que se ubica en la Cooperativa Agraria Atahualpa Jerusalén, comúnmente denominada Granja Porcón. Entre las coordenadas UTM 760796 - 763180 Este y 9217799 – 9218875 Norte de la proyección WGS 84-Zona 17S, y con un rango altitudinal entre 3530 y 3620 msnm (Figura 1).

El macizo forestal tiene una edad de 30 años, instalado sobre una superficie de 122 ha en un sistema de plantación de tres bolillos con un distanciamiento de 3 x 3 m, cuenta con un raleo a los diez años a una intensidad de 38%. Los suelos son derivados de materiales volcánicos, recubiertos de un espeso horizonte orgánico, el pH fluctúa entre 4.5 y 5.5; siendo ricos en nitrógeno, pobres en fósforo y con altas cantidades de aluminio (Pajares et al. 1984). Basándose en el registro de 17 años de la estación meteorológica de Granja Porcón, ubicada a 3 km del área de investigación, la temperatura promedio, mínima y máxima son de 8.1 °C, 2.3 y 13.9 °C respetivamente; con una precipitación de 1179.5 mm/año, presentándose las mayores precipitaciones de octubre a abril y la humedad relativa promedio es de 68% (SENAMHI, 2018).

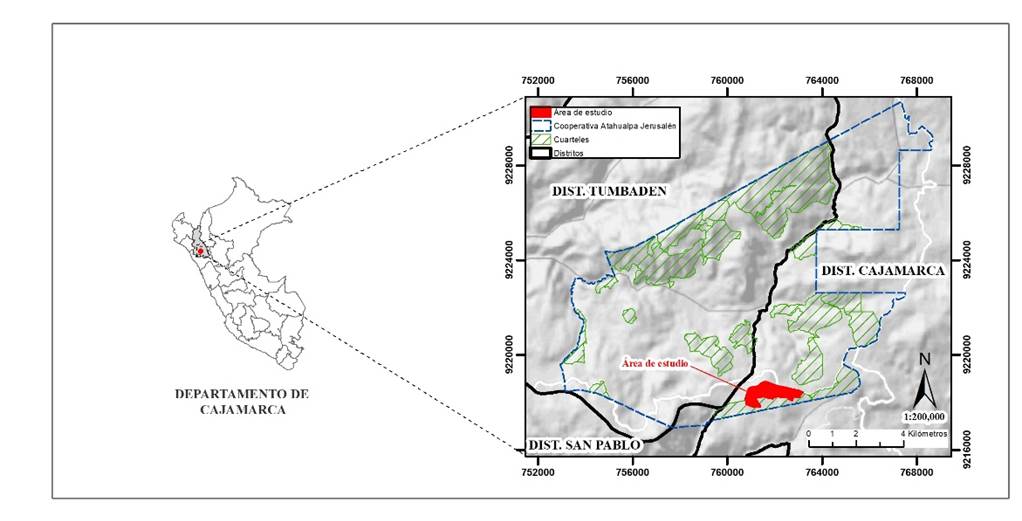
Figura 1. Área de investigación.

2.2. Metodología

Para determinar los volúmenes maderables del macizo forestal se realizó un muestreo al azar, instalándose en total diez parcelas rectangulares de 20 m x 50 m (1 000 m²), donde se midió el DAP y la altura total (Ht) y comercial (Hc), esta última variable dasométrica fue considerada hasta donde el fuste puede ser utilizado para aserrío. 

Se comparó el grado de estimación de cuatro modelos (1- 4), del total de árboles mensurados se eliminaron aquellos datos que no contribuían a la regresión (outliers – árboles bifurcados) quedando al final 465 árboles. El ajuste de los modelos fue realizado con el Software Statistica 13, mediante el método de mínimo cuadrados. La validación de las regresiones se realizó con las pruebas de “F” y “t” a una significancia de ∝ ≤0,05 y un 95 % de confianza. El mejor modelo fue escogido en función al coeficiente de correlación (R(Y ̂Y)), Coeficiente de determinación (R²), error padrón residual  (S_y x), y también al análisis gráfico de distribución de residuos.

……………..…………….(1)

……………….(2)

 …………...………...…. (3)

……….(4)

Siendo: 𝑉𝑇/𝐶=𝑉𝑜𝑙𝑢𝑚𝑒𝑛 𝑡𝑜𝑡𝑎𝑙 𝑜 𝑐𝑜𝑚𝑒𝑟𝑐𝑖𝑎𝑙, en m³; 𝐷𝑎𝑝=𝐷𝑖á𝑚𝑒𝑡𝑟𝑜 𝑎 𝑙𝑎 𝑎𝑙𝑡𝑢𝑟𝑎 𝑑𝑒𝑙 𝑝𝑒𝑐h𝑜, en cm; H𝑇/𝐶=𝐴𝑙𝑡𝑢𝑟𝑎 𝑡𝑜𝑡𝑎𝑙 𝑜 𝑐𝑜𝑚𝑒𝑟𝑐𝑖𝑎𝑙, en m; 𝛽₀, 𝛽₁, 𝛽₂= Constantes propias del modelo de regression.

Los datos obtenidos en el inventario fueron sistematizados y procesados en el software Excel, obteniendo el volumen total (VT), volumen comercial (VC), el Incremento Medio Anual total (IMAt) y el Incremento Medio Anual comercial (IMAc) existente en cada parcela, los cuales fueron promediados y extrapolados para estimar sus valores por ha. El volumen maderable del macizo forestal fue determinado usando los datos volumétricos por ha y la extensión boscosa, este último dato fue estimado usando el programa ArcGIS mediante una clasificación supervisada, obteniéndose el área neta de la plantación.

Para calcular el porcentaje de error (E%) del inventario se usó la fórmula mencionada por Soares et al. (2011) para determinar el número de parcelas en poblaciones finitas, plantaciones, usando los VT y VC de las parcelas y se estimó la relación error de muestreo y número de parcelas. El valor de “t” fue determinado a un nivel de probabilidad de 95% y 9 grados de libertad (número de parcelas – 1); y el valor de N es la división del área total de la plantación entre el área de una parcela (ha).  

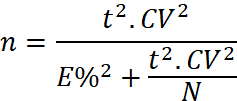
Donde: n=tamaño de muestra, t= valor estadístico tabulado, “t” de Student; CV= Coeficiente de variación (%) de los volúmenes por parcela; E= error admisible, %; N= número de unidades muestrales

3. RESULTADOS Y DISCUSIÓN

Los modelos ajustados son estadísticamente significativos. tanto para la prueba de “F” como para la prueba de “t”. tal como se puede observar en la Tabla 1. Producto del ajuste se obtuvieron los valores de los parámetros mostrados en la Tabla 2.

Tabla 1. Análisis de varianza de las regresiones

Variables dasométricas			Volumen total				Volumen comercial
Modelo			1	2	3	4	1	2	3	4
Grados de libertad	Regresión		1	2	1	1	1	2	1	1
	Residuos		463	462	463	463	463	462	463	463
	Total		464	464	464	464	464	464	464	464
Calculado	“F”		2932.449	9072.054	3354.421	9167.421	1291.074	4428.939	1417.249	20300.735
	“t”		-30.534	-83.495	-7.422	-92.743	-25.348	-46.489	-15.281	-156.952
			54.152	104.506	57.917	95.750	35.932	39.592	37.646	142.480
				45.553				44.700
Tabulado	“F”		3.984	2.99	3.984	3.984	3.984	2.99	3.984	3.984
	“t”		2.576

Tabla 2. Parámetros de los modelos

Variables dasométricas		Volumen total				Volumen comercial
Modelo		1	2	3	4		1	2	3	4
Parámetros		-1.938	-3.067	-0.226	-4.303		-1.453	-1.188	-0.430	-3.253
		0.090	0.079	0.001	1.571		0.054	0.032	0.001	1.237
			0.086					0.081

El ajuste de todos los modelos presenta muy buenos indicadores estadísticos. tanto para VT como para el VC. Siendo el menor R_(Y ̂Y) de 0.858 y el máximo Error padrón residual de 0.641 (Tabla 3). El modelo 4 estimó mejor los volúmenes maderables (VT y VC), presentando en el gráfico de distribución de residuos homogeneidad de varianza, que en su mayoría no superó el 20 % de error (Figura 2).

Tabla 3. Indicador estadístico del grado de ajuste

Variables dasométricas		Volumen total				Volumen comercial
Modelo		1	2	3	4	1	2	3	4
Indicador		0.929	0.988	0.937	0.975	0.858	0.975	0.868	0.988
	R^2	0.864	0.975	0.879	0.951	0.736	0.950	0.754	0.977
		0.203	0.641	0.617	0.636	0.321	0.361	0.324	0.355

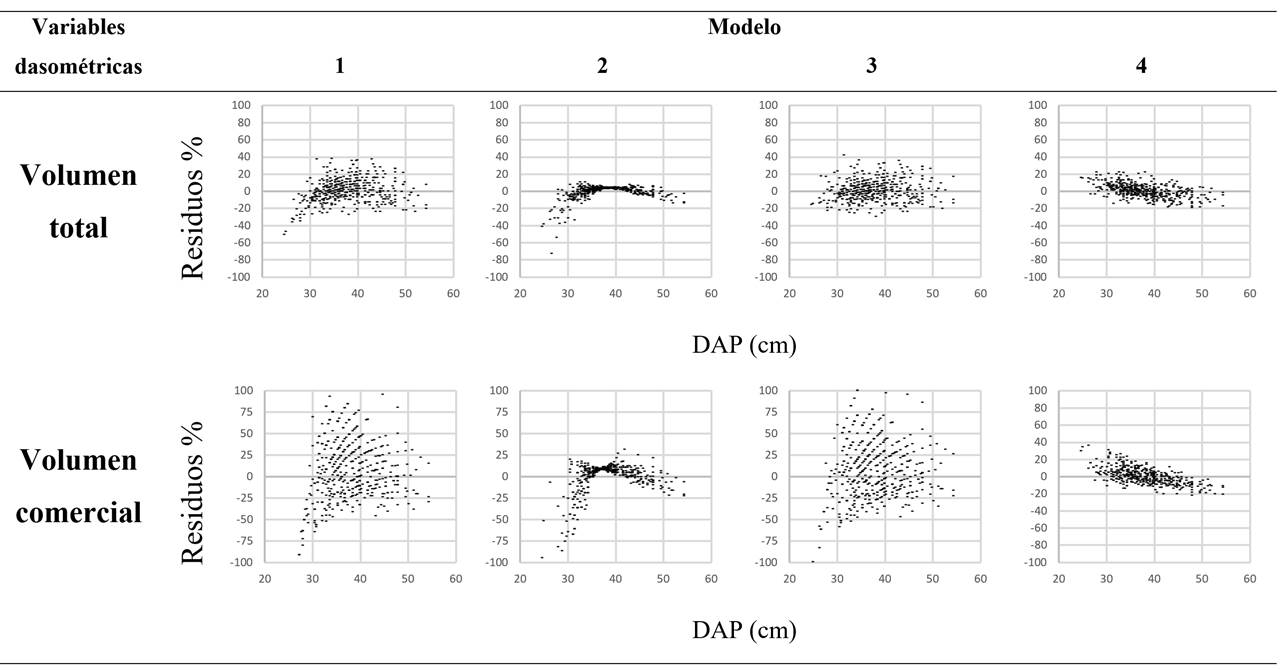
Figura 2. Gráficos de distribución de residuos.

En la Tabla 4 se muestran 11 clases diamétricas, en donde se observa que el mayor número de árboles se encuentra concentrado principalmente en las clases de 32 – 36 y 36 – 40 cm de DAP con 26.8 y 23.7 %; y en menor número en clase 60 – 64 y 56 – 60 cm de DAP con 0,2 y 0 %. La distribución diamétrica presenta una tendencia normal (Figura 3).

Tabla 4. Clases diamétricas del macizo forestal

Intervalos de clase	Marca de clase	N° de árboles	Frecuencia relativa (%)
20 – 24	22	3	0.6
24 – 28	26	20	4.1
28 – 32	30	57	11.8
32 – 36	34	129	26.8
36 – 40	38	114	23.7
40 – 44	42	82	17.0
44 – 48	46	44	9.1
48 – 52	50	26	5.4
52 – 56	54	6	1.2
56 – 60	58	0	0.0
60 – 64	62	1	0.2
		482	100

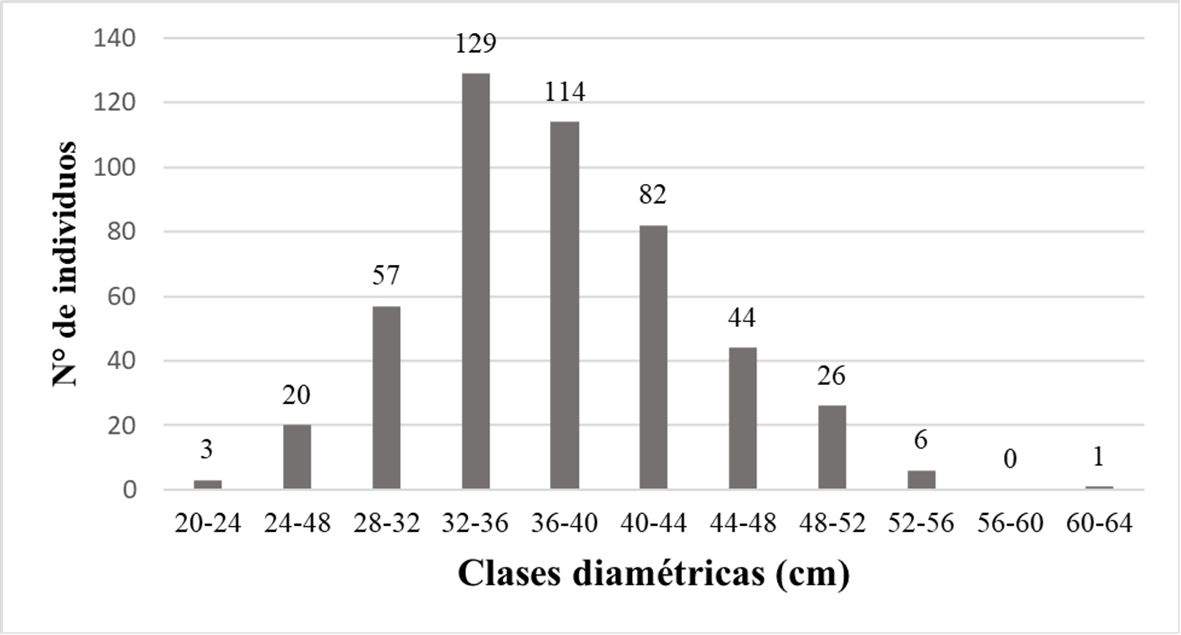
Figura 3. Distribución diamétrica.

En la Tabla 5 se observan los resultados obtenidos en cada parcela evaluada; donde el DAP y la altura total presentaron homogeneidad, caso contrario el VC y el IMAc fueron las variables dasométricas con mayor heterogeneidad. Con respecto a los volúmenes por ha se obtuvo un VT de 718.4397 m³ha^-1 y VC de 277.0618 m³ha^-1 un IMA_t de 23.9480 m³ha^-1año^-1 y un IMAc de 9.6383 m³ha^-1año^-1. Mediante la clasificación supervisada se estimó que el área boscosa es de 108 ha, por lo tanto, el macizo forestal tiene 77591.49 m³ de VT y 2586.39 m³ de VC.

Tabla 5. Variables dasométricas por parcela

Parcela	N° árboles	DAP (cm)	HT (m)	HC (m)	AB (m^2)	VT (m^3)	VC (m^3)	IMAt (m^3año^-1)	IMAc (m^3año^-1)
1	58	38.8	18.7	9.6	7.0413	93.4305	48.2659	3.1143	1.6089
2	47	38.6	22.2	9.5	5.7256	89.9882	39.7144	2.9996	1.7267
3	26	45.0	20.9	10.4	4.1769	61.4333	30.8522	2.0478	1.0284
4	64	37.4	16.6	7.1	7.1758	83.3692	36.8921	2.7790	1.2297
5	45	37.9	17.2	6.5	5.1736	62.3495	24.1929	2.0783	0.8064
6	49	35.9	18.2	5.6	5.0293	64.3997	20.5472	2.1467	0.6849
7	55	38.1	16.8	5.7	6.4049	75.9497	27.0208	2.5317	0.9007
8	41	36.2	18.1	5.2	4.3715	55.9277	17.0776	1.8643	0.5693
9	49	35.8	18.6	5.2	5.0194	65.3484	19.0474	2.1783	0.6349
10	48	32.6	20.7	4.1	4.0960	66.2435	13.4512	2.2081	0.4484
Media	48	37.6	18.8	6.9	5.4214	71.8440	27.7062	2.3948	0.9638
Des. Estand.	10	3.2	1.9	2.2	1.1327	13.0201	11.1375	0.4340	0.4358
Max.	64	45.0	22.2	10.4	7.1758	93.4305	48.2659	3.1143	1.7267
Min.	26	32.6	16.6	4.1	4.0960	55.9277	13.4512	1.8643	0.4484
C.V.	21	8.5	10.0	32.0	20.8924	18.1227	40.1985	18.1227	45.2125

Con respecto a los errores de estimación obtenidos con 10 parcelas son de 12.9 % y 28.6 % para el VC y VT respectivamente, así mismo se observa a medida que se incrementa el número de parcelas de muestreo, el error disminuirá (Figura 4).

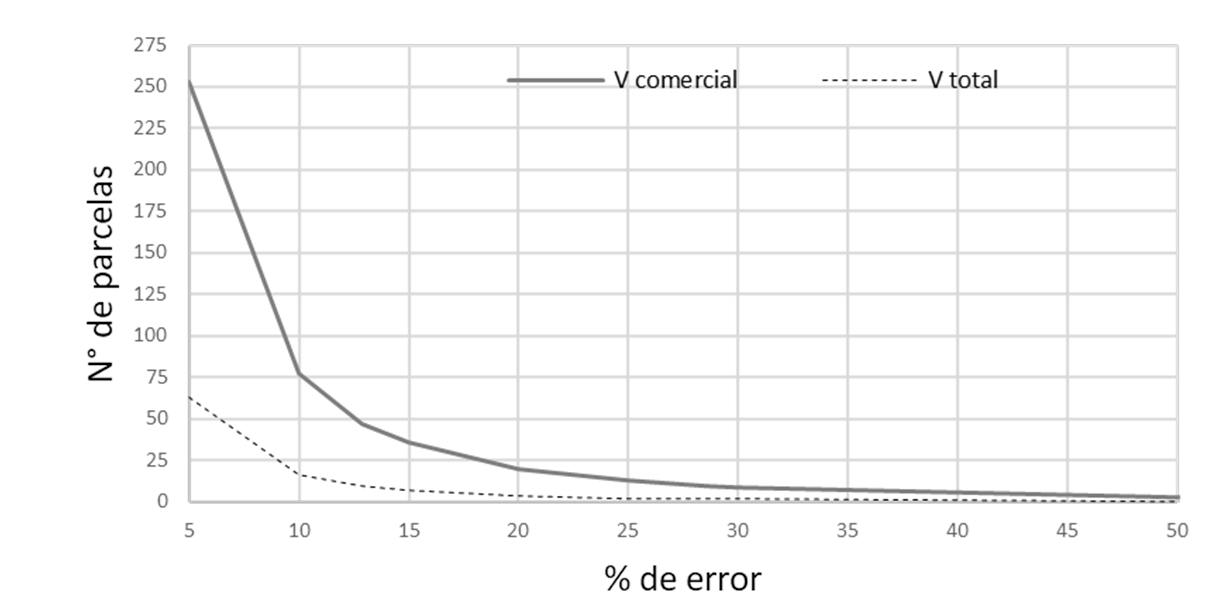
Figura 4. Relación Error y número de parcelas.

Los modelos que tuvieron mejores ajustes fueron el 2 y 4, reflejándose en sus buenos indicadores estadístico, donde el menor Coeficiente de determinación fue de 0.950; estos valores estan cercanos a los obtenidos por Ramos et al. (2014) para Pinus lawsonii y Pinus Oocarpa con los modelos de Schumacher-Hall, Thornber y Spurr con valores para el R² ajustado entre 0.97 a 0.99. Según Cailliez (1980) la calidad de una regresión no solamente se debe jugar por el valor numérico, el ajuste puede ser malo y el valor de R² elevado. Picard et al. (2012) además mencionan que en los ajustes de modelos de volumen o biomasa la hipótesis más importante es la constancia de varianza de los residuos. El modelo 2 presentó subestimaciones en diámetros menores teniendo una distribución heterocedastica de sus residuos, caso contrario presentó el modelo 4 con una varianza constante de sus residuos (homocedastica); determinándose que el modelo  expresa mejor los volúmenes de cada árbol en la plantación. Además, se puede observar que los ajustes de todos los modelos para el VC presentaron menor precisión de estimación que para el VT debido a la variación existente del parámetro dasométrico VC al nivel de individuos.

El macizo presenta una distribución diamétrica normal de una plantación se puede observar en la Figura 01 que existe un mayor número de individuos sobre la media que es de 37.62 lo cual es producto de raleo efectuado a los 10 años. Por otro lado, Mendo (2008) reportó en otro macizo de la misma especie de 21 años en Granja Porcón que el VT es de 347.97 m³ ha-1 y el VC es de 272.36 m³ ha^-1, representado este último un 78.3 % del primero; con los resultados obtenidos esta relación baja hasta un 38.6 % debido a que el diámetro mínimo para aserrío se encuentra a menor altura en el árbol que en promedio es de 6.9 metros.

La descripción más precisa de una población es el resultado de mediciones detalladas de todos sus miembros (censo forestal), este tipo de estudio suele ser imposible debido a su alto costo y problemas logísticos; la solución es la muestra que mide una parte representativa de la población y estos datos recopilados son extrapolados a la población (Roberts et al., 1992). Los diseños de inventarios forestales están orientados principalmente para obtener estimaciones confiables de las masas boscosas en relación a las superficies que ocupan mediante parcelas de muestreo (Alder 1980).

La precisión de estimación de un inventario está en función del objetivo para el cual se requiere la información. Leite y Campos (2013) mencionan que un inventario pre-corte exige una alta exactitud ya que los datos obtenidos serán usados para determinar el recurso financiero, humano y materiales; citando para plantaciones un error de 10% y para bosque naturales de 15%.  El mayor error de estimación en el muestreo del VC se debe a que presenta mayor heterogeneidad por parcela como se observa en la Tabla 2 con un coeficiente de variación de 40 %; si el inventario realizado tuviera un fin de pre-corte se hubiera necesitado instalar en total 77 parcelas para estimar el VC y 16 parcelas para el VT.  En plantaciones más uniformes al no existir mucha variación la población estaría representada con un menor número de parcelas.

4. CONCLUSIONES

Los volúmenes de madera por ha fueron de 718.4397 m³ para el VT y de 277.0618 m³ para el VC representando este último un 38.6 % del primero; esta relación es baja pero aun así existe madera que tiene un valor comercial para otras industrias como para postes o tableros.

Los ajustes que presentaron mejores estimaciones son  y  obteniéndose un  mínimo de 0.975 un máximo de 0.636 y varianza constante en sus residuos; estas regresiones pueden ser usadas para estimar volúmenes de árboles de macizo con las características iguales a la zona donde se realizó la investigación o el modelo puede dar buenos ajustes para masas boscosas con otras condiciones y especies forestales.

Declaración de intereses

Ninguna.

Referencias

ADEFOR (Asociación Civil para la Investigación y Desarrollo forestal, Perú) (1996). Manual zonificación de especies y plantaciones forestales. Cajamarca, Perú.  90 p.

Alder, D. (1980). Estimación de volumen forestal y predicción del rendimiento: con referencia especial a los trópicos, Roma, Organización de las Naciones Unidas para la Alimentación y la Agricultura. 80 p.

Cailliez, F. (1980). Estimación de volumen forestal y predicción del rendimiento con referencia especial a los trópicos, Roma, Itália, Organización de las Naciones Unidas para la Alimentación y la Agricultura. 92 p.

Campos, J. (1970). Estudo sobre índice de sítio e tabelas de volume e produção para Pinus elliottii Engelm no estado de São Paulo. Teses Mag. Sc. San José. CR. Instituto Interamericano de Cooperación para la Agricultura (IICA). 95 p.

Campos, J.C.C. & Leite, H.G. (2013). Mensuração Florestal: Perguntas e Respostas. 4 ed. Viçosa. Minas Gerais, Brasil. Universidad Federal de Viçosa. 605 p.

Carton, C. (1996). Reforestación y manejo de cuencas en la CAT. Atahualpa Jerusalén. Granja Porcón, Cajamarca. En Adefor, Manejo integral de microcuencas. Jequetepeque - Cajamarca (pp. 185-195).

CIFAFOR (Centro de Investigación y Capacitación Forestal, Perú) (1982). Datos meteorológicos correspondientes: periodo de años y año 1985. Cajamarca. Perú.  60 p.

Del Pozo, F.A. (1996). Factor de conversión de aserrío para productos de raleo en plantaciones de Pino patula en Cajamarca. Tesis ingeniero Forestal. Lima, Perú. Universidad Nacional Agraria la Molina. 91 p.

Dvorak, W.S., Hodge, G.R., Kietzka, J., Malan, F., Osorio, L. F. & Stanger, T.K. (2000). Pinus patula. In: Conservation and Testing of Tropical and Subtropical Forest Tree Species. CAMCORE Cooperative, College of Natural Resources. NCSU Raleigh. NC. USA. 148-173 p.

FAO (Organización de las Naciones Unidas para la Alimentación y la Agricultura, Roma). (2016). Los bosques y el cambio climático en el Perú. Roma. Italia. 142 p.

Higuera, C. (1994). Funciones de volumen y ahusamiento para Roble Nothofagus obliqua (MIRB. OERST) y Gualo Nothofagus glauca (PHIL. KRASER). Tesis de maestría. Universidad Austral de Chile. 74 p.

Mendo, M.H. (2008). Valoración económica de los bienes y servicios ambientales del bosque Granja Porcón. Cajamarca-Perú. Tesis de doctorado. Lima, Perú. Universidad Nacional de Trujillo. 86 p.

Ospina, C., Hernández, R., Rincón, E., Sánchez, F., Urrego, J., Rodas, C., Ramírez, C., Riaño,, N. (2011). Guías silviculturales para el manejo de especies forestales con miras a la producción de madera en la zona andina colombiana: El Pinus patula Schl et Cham. FNC-Cenicafé. Colombia.

Pajares, T.G., Poma, R.W. & Vega, B.M. (1984). Estudio detallado de los suelos de suelos de 22 arbotera en Cajamarca. Cajamarca, Perú. CICAFOR (Centro de Investigación y Capacitación Forestal. Perú). 124 p. 

Picard, L. & Villar, C.M. (1986). Metodología utilizada para la introducción de especies forestales en Cajamarca - Perú. Cajamarca, Perú. CICAFOR (Centro de Investigación y Capacitación Forestal, Perú). 70 p. 

Picard, N., Saint-André, L. & Matieu, H. (2012). Manual de construcción de ecuaciones alométricas para estimar el volumen y la biomasa de los árboles. Roma, Itália. Organización de las Naciones Unidas para la Alimentación y la Agricultura. 223 p.

Ramos, J.A., García, M.J., Hernández, R.J., García, C.X., Velarde, J.C., Muñoz, H.J. & García, G.G. (2014). Ecuaciones y tablas de volumen para dos especies de Pinus de la sierra Purhépecha. Michoacán. Revista Mexicana de Ciencias Forestales, 5(23): 92 -109.

Roberts, R.E., Tomppo, E.O. & Czaplewski, R.L. (1992). Diseños de muestreo de las Evaluaciones Forestales Nacionales. Organización de las Naciones Unidas para la Alimentación y la Agricultura. 21 p. 

Soares, C.P.B., Paula, N.F. & Souza, A.L. (2011). Dendrometria e Inventário Florestal. 2. ed. Viçosa. Minas Gerais, Brasil. Universidad Federal de Viçosa. 272p.