Biomasa y secuestro de carbono radicular, en bosque natural de “algarrobo” en el campus de la Universidad de Piura (UDEP)
Biomass and root carbon sequestration, in natural forest of "carob tree" on the campus of the University of Piura (UDEP)
Duber Orlando Chinguel Laban1*![]() , Jesús Manuel
Charcape Ravelo1
, Jesús Manuel
Charcape Ravelo1 ![]()
1 Universidad Nacional de Piura, Piura, Perú
*Autor de Correspondencia, e-mail investigafep@lamolina.edu.pe
Recibido, 25/11/2019 Aceptado, 01/12/2019 DOI:10.25127/aps.20193.502

RESUMEN
El presente trabajo tiene como objetivo estimar la biomasa y el carbono radicular secuestrado, a través de estimaciones directas e indirectas. Para esto se aplicó el método directo, el cual consistió en la extracción de la raíz, luego el pesado de las muestras de cada componente o secciones diamétrica establecidas en el muestreo y de manera indirecta se usaron ecuaciones alométricas. Se seleccionaron 25 árboles previamente cortados, los cuales solo se mantenían en tocón. Al extraer la raíz, se realizaron mediciones de 4 secciones diamétricas (0,5-2cm; 2-5cm; 5-10cm; y >10cm), cortando 3 rodajas de 5cm de espesor por cada una de las secciones diamétricas. En campo se determinó el peso fresco, tanto de la muestra de cada sección diamétrica, como de las rodajas de las secciones diamétricas. Estas muestras (rodajas) fueron llevadas al laboratorio para obtener su peso seco, y luego elaborar las ecuaciones alométricas mediante regresiones simples. La biomasa total radicular, estimada mediante la ecuación alométrica aplicada a los 359 árboles, en las 6 parcelas de 50x50 m, arrojó un total de 3806,2 kg de biomasa. Como el bosque natural de algarrobo de la Universidad de Piura, tiene un área de 50 ha, la biomasa total radicular fue de 126,8 t/ha y el carbono radicular secuestrado total fue de 63,33 tC/ha.
Palabra clave: biomasa radicular; secuestro de carbono; ecuación alométrica.
ABTRACT
The present work aims to estimate biomass and sequestered root carbon, through direct and indirect estimates. For this purpose, the direct method was applied, which consisted on the extraction of the root, then the weighing of the samples of each component or diameter sections established in the sampling and in an indirect way, alometric equations were used. Twenty-five previously cut trees were selected, which were only kept in stumps. When extracting the root, measurements were made of 4 diameter sections (0.5-2cm; 2-5cm; 5-10cm; and >10cm), cutting 3 slices of 5cm thickness for each of the diameter sections. In the field, the fresh weight of both the sample of each diameter section and the slices of the diameter sections was determined. These samples (slices) were taken to the laboratory to obtain their dry weight, and then to elaborate the allometric equations by means of simple regressions. The total root biomass, estimated by means of the allometric equation applied to the 359 trees, in the 6 plots of 50x50 m, yielded a total of 3806.2 kg of biomass. As the natural forest of carob tree of the University of Piura, has an area of 50 ha, the total root biomass was 126.8 t / ha and the total root carbon sequestered was 63.33 tC / ha.
Key words: radicular biomass, carbon absorption, allometric equation.
I. INTRODUCCIÓN
Los bosques, como un sistema natural complejo, contribuyen a mitigar el cambio climático al almacenar carbono en la vegetación y en el suelo. Intercambiar carbono con la atmosfera, a través del proceso fotosintético y la respiración. Estos se convierten en fuente de carbono para la atmósfera, cuando sufren alteraciones provocadas por el hombre o por causas naturales, por ejemplo, actividades de conversión de bosque a otros usos no forestales (Trumper et al., 2008).
Actualmente, cerca de un 20% de emisiones de CO2 en la atmosfera resultan de la eliminación y/o degradación de los ecosistemas forestales. La detención y reversión de la deforestación, a través de la reforestación y manejo sustentable, implica secuestrar el CO2, disminuir la concentración de gases de efecto invernadero en la atmosfera y reducir el calentamiento global (Schlegel, 2001).
Los proyectos de secuestro de carbono que se generan en el marco del mecanismo para un desarrollo limpio, establecido en el protocolo de Kioto, requieren de información básica solida sobre las plantaciones forestales y su biomasa. Debe estar fundamentada sobre evaluaciones cuantitativas confiables. Tanto las metodologías, como las propias mediciones de la biomasa forestal y los inventarios de monitoreo son la base de confianza de toda negociación de proyectos de captura de emisiones GEI (Guerra, 2001).
Así en el departamento de Piura en Perú, los bosques de algarrobo ocupan alrededor de un millón de hectáreas (GRP, 2010). Los algarrobales, ocupan las planicies costeras y las partes bajas de las estribaciones de la cordillera. La Torre-Cuadros y Linares (2008) han identificado dos tipos de comunidades vegetales dominadas por el algarrobo: un bosque estacionalmente seco que crece por debajo de los 100 m.s.n.m y un bosque estacionalmente seco de franja inferior de montaña que crece entre los 100 y 400 m.s.n.m. Por lo tanto, la estimación adecuada de la biomasa de un bosque, es un elemento de gran importancia debido a que esta permite determinar los montos de carbono y otros elementos químicos existentes en cada uno de sus componentes y representa la cantidad que puede ser liberado a la atmósfera, conservado y fijado en una determinada superficie (Brown et al., 1996).
A partir de la biomasa forestal, se puede calcular la concentración de carbono en la vegetación (aproximadamente el 50% de la biomasa está formada por carbono) y por consiguiente se pueden hacer estimaciones sobre la cantidad de dióxido de carbono que ingresa a la atmosfera, cada vez que se desmonta o se quema un bosque. La biomasa es una variable, que sirve también para comparar las características estructurales y funcionales de un ecosistema forestal en un amplio abanico de condiciones (FAO, 2001; Vidal et al., 2003). Esta información es de especial importancia, debido a la necesidad de conocer los montos de carbono secuestrado por los bosques naturales y plantaciones, como un medio para mitigar los cambios climáticos generados por el consumo de combustibles fósiles, entre otros (Schlegel et al.,2000).
Para el análisis de la biomasa radicular, actualmente existen dos métodos para cuantificar la biomasa y por ende el carbono secuestrado. Primero tenemos el método directo, el cual es complejo y exige mucho esfuerzo de tiempo y recursos en campo (Cairns et al., 1997, Clark et al., 2001). Por esta razón, la información relacionada con los contenidos de carbono que se presentan en este compartimiento y en los bosques naturales, aún se encuentra pobremente estimada (Clark et al., 2001). El otro método es el indirecto, que sugiere hacer estimaciones, con respecto a la biomasa aérea, Cairns et al. (1997), para la relación raíz/tallo (R/T), entrega valores entre el 20 y 30% de biomasa radicular con respecto a biomasa aérea.
En proyectos de secuestro de carbono en ecosistemas forestales, no realizan mediciones en comportamiento subterráneo, por la dificultad en su extracción y los altos costos que demanda. Por tanto, se usan valores reportados en literatura (MacDicken, 1997, Salimon y Brown, 2000, Brown et al., 1999, De Jong et al., 2000). De esta manera, se opta por el método indirecto el cual se convierte en una opción para estimar los contenidos de carbono a partir de la información obtenida de la biomasa aérea, particularmente para proyectos a gran escala.
El objetivo de la investigación fue estimar la biomasa y el carbono radicular secuestrado en el bosque natural de algarrobo en campus de la Universidad de Piura, a través de estimaciones directas e indirectas.
II. MATERIAL Y MÉTODOS
Ubicación del área de estudio
El área de estudio se ubica en el campus de la Universidad de Piura, ubicado en el Distrito de Piura, Provincia y Departamento de Piura en una Latitud de 5°10´11” S y de longitud 80° 36´51” W (Figura 1).
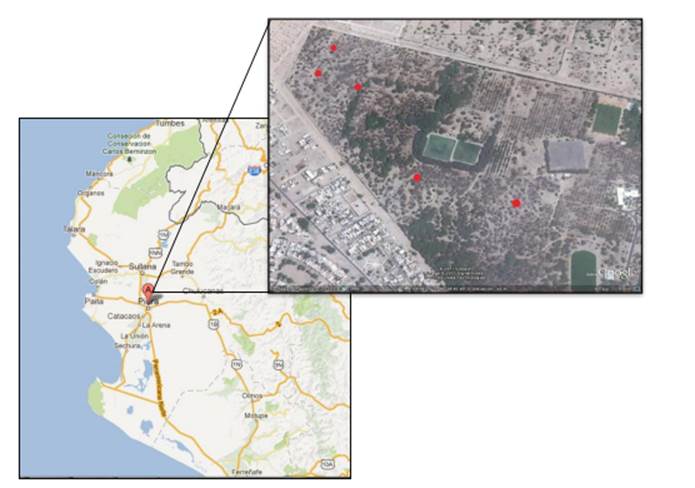
Figura 1. Área de estudio en la Universidad de Piura.
Descripción del área de estudio
Suelo
La zona de estudio se encuentra conformado por material de relleno (desmonte, entre ladrillos y piedras, los primeros 30 cm de profundidad), arena fina limosa suelta, arena fina limosa medianamente densa, arena fina limosa densa, arcilla arenosa compacta, arcilla con arena fina compacta (IN, 2008).
Clima y Vegetación.
El bosque natural de algarrobo del campus de la UDEP, pertenece a la Ecorregión del Bosque Seco Ecuatorial (Brack, 1988). La vegetación dominante es Prosopis pallida, con algunas formaciones abiertas de Acacia macracantha, Parkinsonia aculeata, entre otras. Las temperaturas máximas llegan a 34,2° C y las mínimas a 15°C respectivamente. La humedad promedio anual es del 66%, con una velocidad de viento de 3m/s. Las precipitaciones pluviales llegan a los 59,6 mm (CA, 2004). En los muestreos de extracción de raíces se realizaron entre junio-octubre del 2012, siendo las temperaturas como máximo de 30,3°C y mínima de 17,8°C, la humedad promedio estuvo en 70,6%.
Diseño muestreo
La unidad de muestreo que se utilizó para la recopilación de datos fue adaptada en base al esquema utilizado por el proyecto Algarrobo en Perú, para ello se usaron parcelas cuadradas de un tamaño de 50 x 50 m. La ubicación de las parcelas se realizó a través de un mapa del área del bosque natural de algarrobo del campus de la Universidad de Piura. Posteriormente se dividió en cuadrantes, a los cuales se le asignó un número. Para la selección aleatoria simple de la ubicación de una parcela, se realizó un sorteo entre los números que representaron a las parcelas, seleccionado un total de 6 Parcelas (Figura 2).
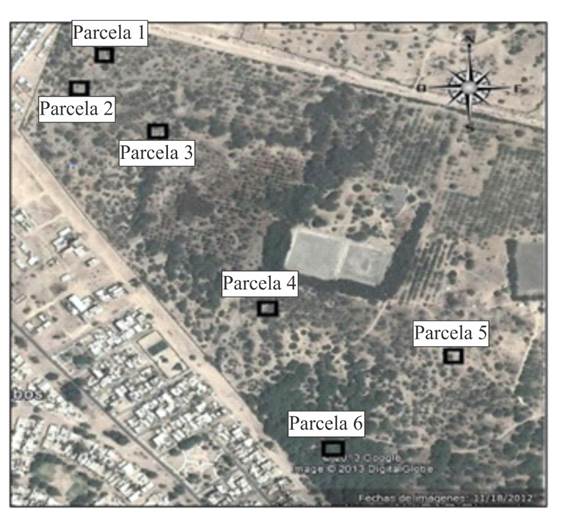
Figura 2. Ubicación de las parcelas distribuidas en el bosque de algarrobo del campus de la Universidad de Piura.
Cálculos de biomasa y carbono radicular
Para estimar el carbono en la biomasa radicular, se usaron las parcelas de 50 x 50m antes mencionadas y los datos dasométricos de Diametro a la Altura de Pecho (DAP) y altura de los árboles contenidos en las mismas, las cuales se utilizaron para la elaboración de las ecuaciones alométricas. Los valores de la biomasa fueron obtenidas a través de cálculos utilizando las ecuaciones alométricas que se elaboraron para los diferentes diámetros de la raíz. Finalmente, para estimar la cantidad de carbono en la biomasa total de las raíces, se utilizó, la siguiente formula.

Donde:
CBR=Carbono en la biomasa radicular total (t/ha)
BRT= Biomasa radicular total
0,5 = Fracción de carbono en la biomasa (IPCC, 1994)
Determinación de la ecuación alométrica
Para la determinación de la ecuación alométrica, se siguió el modelo para la biomasa aérea de Llanos (2010). Se talaron 25 árboles, a una altura promedio de 32 cm para quedar solamente los tocones. En estos árboles se tuvo en cuenta la abundancia de individuos por clases diamétricas en cada parcela, los cuales fueron seleccionados mediante un sorteo al azar.
Posteriormente, se identificaron los tocones, y a la vez se determinó la zona de influencia de raíces (ZIR), sobre la cual se trabajó removiendo el suelo, para así extraer de forma cuidadosa las raíces. Se definieron los radios de acción para límites de trabajo, según el DAP del árbol. Todo ello según la metodología propuesta por Schlegel et al. (2000). Tras la extracción, se procedió a la medición y pesado de las raíces. Para ello, se realizó una serie de mediciones de diámetros determinados de 0,5; 2; 5 y >10 cm de diámetro. En donde la raíz se dividió en líneas imaginarias y en cada uno de ellos se realizó mediciones de las raíces. Luego, se cortó la raíz diferenciando cuatro subdivisiones (secciones diamétricas), entre 0,5 - 2 cm; entre 2 - 5 cm; entre 5 - 10 cm y una sección mayor a 10 cm de diámetro radicular (tocón radicular). Primero se separaron las raíces delgadas y medianas con un serrucho de mano, luego se separarán las raíces gruesas. Posteriormente se pesaron en una balanza de mano de 1kg y una de reloj de 5kg Roma, por separado y se tomaron los valores.
Para la determinación del peso seco de las raíces, se extrajeron muestras de cada tipo de raíz (delgada, media y gruesa). Se tomaron mediante el método aleatorio simple, 3 muestras de raíces (entre 0,5 - 2 cm de diámetro), 3 muestras de raíces (entre 2 - 5 cm de diámetro) y 3 de raíces (entre 5 - 10 cm de diámetro) de 5 cm de espesor de cada una de ellas, así como también 3 muestras de raíces >10cm.Posteriormente las rodajas (5cm de espesor) se rotularon con los datos de lugar de extracción, con su respectiva codificación, numero de parcela y número del árbol. Las muestras fueron llevadas al edificio de Química de la Universidad de Piura, donde se pesaron en una balanza analítica, antes de proceder a su secado. El secado de todas las muestras fue hasta determinar su peso seco constante, en el proceso de secado la temperatura fue de 120°C, las muestras se pesaron por lapsos de tiempo a las 10 y 12 horas, este procedimiento termino cuando todas las muestras obtuvieron un peso seco constante.
Luego de tener el peso constante de las muestras, se calculó el contenido de humedad radicular, utilizando la siguiente relación:
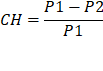
Donde:
CH= Contenido de humedad
P1= Peso húmedo de la muestra obtenida en campo
P2= Peso seco constante de la muestra obtenida en la estufa.
Para la determinación del porcentaje del contenido de humedad de cada sección de la raíz.
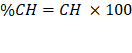
Donde:
CH= Contenido de humedad
%CH= Porcentaje del contenido de humedad
Posteriormente se determinó el peso seco total de cada sección de la raíz. Teniendo registrado el peso húmedo total (de campo) de los componentes de cada sección (diámetros) de la raíz y con el contenido de humedad hallado, se determinó el peso seco total de cada sección de la raíz.

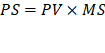
Donde:
MS= Materia seca
CH= Contenido de humedad
PS= Peso seco total
PV= Peso verde o húmedo total de campo
Mediante el uso del programa estadístico Statgraphics Centurion versión 15, se realizaron las regresiones lineales simples y múltiples respectivas. Se consideró como variable dependiente a la biomasa seca, hallada para cada los diámetros (0,5 - 2; 2 – 5; 5 – 10; ≥10) y la biomasa radicular total. Los datos dasométricos, como el DAP y la altura, se consideraron como variables independientes. Mediante las regresiones mencionadas al inicio se fueron obteniendo las diferentes ecuaciones para cada sección de diámetros.
De las ecuaciones obtenidas mediante el programa estadístico Statgraphics, se descartaron aquellas que tuvieron R2 y R2 ajustado, cercanos a cero, así mismo se realizó las pruebas de F de Fisher a partir de ANOVA y “t” de Student, mediante estas pruebas se eliminaron las ecuaciones que a través de la primera prueba aceptaron la igualdad de varianzas y a través de la segunda fueron descartadas aquellas que no probaron que bi≠ 0 (Adler, 1980).
Finalmente, de las ecuaciones restantes se seleccionó aquella que tuvo el menor cuadrado medio del error (CME), ya que según Philip (1994) y Llanos (2010) para seleccionar la mejor ecuación de regresión para hacer estimaciones, se debe usar el Cuadrado Medio del Error (CME), del ANOVA de la regresión debido ya que esta será la que representará la mejor predicción sobre la producción de biomasa.
Teniendo la ecuación de biomasa radicular total, esta fue aplicada a cada árbol de las 5 parcelas para lo cual se usaron los valores de las variables independientes de cada uno de estos en la ecuación. Finalmente, ya teniendo la biomasa de todos los árboles, se estimó la cantidad de carbono secuestrado, aplicando la primera ecuación.
Para el cálculo del carbono total secuestrado en raíces, en el bosque natural de algarrobo del campus de la Universidad de Piura, se realizó una extrapolación de datos en los 50 ha del bosque natural de la Universidad de Piura.
Cantidad de dióxido de carbono equivalente
Para calcular el dióxido de carbono equivalente, la cantidad de carbono total secuestrado en raíces del bosque natural, se multiplico por el factor 3,67. Este factor se deriva del peso atómico del CO2. Es decir, la conversión de carbono a CO2 se realizó mediante la siguiente ecuación (Herrera, 2002).
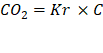
Donde:
CO2 = dióxido de carbono (Kg)
Kr= 3,67 (relación de pesos moleculares de CO2 y C)
C= carbono (Kg)
III. RESULTADOS
Resultados dasométricos
La tabla 1 muestra que el DAP oscilo entre los 2,8cm (árbol 9 de la parcela 3) y los 32,4cm (árbol 32 de la parcela 3), mientras que la altura estuvo entre 2,3m (arboles 9 de la parcela 3) y 9,89m (árbol 40 de la parcela 2).
Tabla 1. Datos dasométricos de los 25 árboles seleccionados
|
N° de Parcelas |
Arboles seleccionados |
DAP (cm) |
Altura (m) |
|
1 |
17 |
6.048 |
4.557 |
|
12 |
7.958 |
3.444 |
|
|
19 |
3.979 |
3.263 |
|
|
56 |
21.486 |
6.377 |
|
|
2 |
77 |
12.128 |
8.643 |
|
35 |
8.626 |
6.817 |
|
|
66 |
8.594 |
5.504 |
|
|
86 |
24.351 |
4.447 |
|
|
30 |
12.828 |
6.381 |
|
|
40 |
9.868 |
9.891 |
|
|
3 |
9 |
2.801 |
2.300 |
|
34 |
6.207 |
3.495 |
|
|
58 |
13.114 |
3.950 |
|
|
32 |
32.468 |
6.695 |
|
|
28 |
20.595 |
3.794 |
|
|
29 |
15.024 |
5.230 |
|
|
22 |
15.597 |
5.062 |
|
|
21 |
7.894 |
5.230 |
|
|
4 |
9 |
16.393 |
6.119 |
|
16 |
30.876 |
8.213 |
|
|
20 |
19.672 |
8.454 |
|
|
52 |
24.351 |
8.454 |
|
|
5 |
32 |
25.146 |
6.119 |
|
18 |
7.003 |
2.341 |
|
|
15 |
11.618 |
4.255 |
Pesos húmedos (PH) totales de cada una de las secciones diametricas
Los diámetros correspondientes a 0.5-2.0cm y 5-10cm, tuvieron un alto peso húmedo total, el mayor peso húmedo, estuvo en el árbol 20, parcela 4 con 6010,26g y el menor peso hallado para la raíz, fue en el árbol 17, parcela 1 con 65,57g (tabla 2 y figura 3).
Tabla 2. Resumen de los pesos húmedos de las secciones diametricas
|
N° de Parcela |
Arboles seleccionados |
PH raíces 0,5-2 (g) |
PH raíces 2-5 (g) |
PH raíces 5-10 (g) |
PH raíces >10(g) |
PH total |
|
1 |
17 |
27.7 |
0.0 |
37.8 |
0.0 |
65.6 |
|
12 |
242.5 |
105.4 |
0.0 |
0.0 |
347.9 |
|
|
19 |
252.3 |
200.2 |
0.0 |
0.0 |
452.5 |
|
|
56 |
80.1 |
0.0 |
0.0 |
0.0 |
80.1 |
|
|
2 |
77 |
41.2 |
11.4 |
0.0 |
0.0 |
52.6 |
|
35 |
18.2 |
282.1 |
171.7 |
0.0 |
472.0 |
|
|
66 |
78.3 |
151.9 |
0.0 |
182.0 |
412.2 |
|
|
86 |
2370.9 |
2025.4 |
535.5 |
151.1 |
5082.9 |
|
|
30 |
88.2 |
36.2 |
0.0 |
0.0 |
124.5 |
|
|
3 |
40 |
125.2 |
370.9 |
102.5 |
138.7 |
737.3 |
|
9 |
35.7 |
30.0 |
0.0 |
0.0 |
65.7 |
|
|
34 |
323.1 |
30.3 |
188.1 |
0.0 |
541.5 |
|
|
58 |
160.0 |
841.5 |
66.8 |
0.0 |
1068.2 |
|
|
32 |
2184.1 |
1744.2 |
1008.6 |
897.2 |
5834.2 |
|
|
28 |
522.7 |
413.4 |
0.0 |
0.0 |
936.2 |
|
|
29 |
610.1 |
274.3 |
327.8 |
0.0 |
1212.2 |
|
|
22 |
300.6 |
144.1 |
242.9 |
0.0 |
543.5 |
|
|
21 |
252.2 |
252.6 |
0.0 |
0.0 |
504.7 |
|
|
4 |
9 |
452.6 |
466.1 |
0.0 |
0.0 |
918.7 |
|
16 |
1917.3 |
876.8 |
1319.2 |
258.0 |
4371.2 |
|
|
20 |
2321.0 |
1988.8 |
771.4 |
929.1 |
6010.3 |
|
|
52 |
1740.8 |
1860.0 |
390.1 |
523.2 |
4514.1 |
|
|
5 |
32 |
1528.0 |
1047.5 |
409.7 |
0.0 |
2985.1 |
|
18 |
334.4 |
108.9 |
0.0 |
0.0 |
443.3 |
|
|
15 |
106.2 |
343.5 |
194.0 |
0.0 |
643.7 |
La cifra 0.0 significa que dicho componente no existía en el árbol
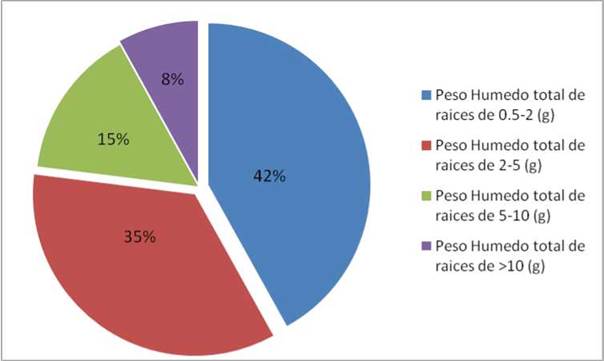
Figura 3. Distribución de los pesos húmedos totales según cada sección diamétrica de la raíz
Relación entre los pesos húmedos de secciones diamétricas de 0,5- 2 cm y 2-5cm
De la relación de los pesos húmedos de las secciones diamétricas de 0,5 - 2 cm y de 2 - 5 cm se observa en la tabla 2, que el peso húmedo de 0,5 - 2 es 11 veces mayor que el 2 -5 (árbol 34, parcela 3), esto se debe a que la raíz de este árbol, presento mayor cantidad de prolongaciones de esta medida. En total de obtuvieron 75 rodajas de secciones de diámetros de 0,5 - 2 (3 rodajas por raíz).
Relación entre los pesos húmedos de secciones diamétricas de 0,5- 2 cm y 5-10cm
De la relación establecida entre el peso húmedo total de las secciones diamétricas de 0.5- 2 y 5¬10cm (tabla 2), se observa que el primero supera hasta 5 veces el peso húmedo total de 5-10cm (árbol 52, parcela 4), esto se debe a que este árbol presenta un mayor número de raíces en los diámetros de 0,5-2cm. En total se obtuvieron 42 rodajas de 5-10cm debido a que no todos los arboles presentaban esos diámetros.
Relación entre los pesos húmedos de secciones diamétricas de 0,5- 2 y >10cm
De la relación establecida entre el peso húmedo total de las secciones diamétricas de 0,5- 2 y >10 (tabla 2), se observa que el primero supera hasta 16 veces el peso húmedo total de >10cm (árbol 86, parcela 2), esto se debe a que este árbol presenta un mayor número de raíces en los diámetros de 0,5-2cm. En total se obtuvieron 21 rodajas de >10cm debido a que no todas los arboles presentaban esos diámetros.
Obtención del peso seco total (PST) de cada sección diamétricas de la raíz
Teniendo el peso seco constante y el contenido de humedad, se calculó la biomasa seca total de cada una de las secciones diamétricas (0,5-2; 2-5; 5-10; >10) y la total. Los resultados obtenidos de la biomasa total de las raíces, se encuentra entre 134,2 g del árbol 17 de la parcela 1 y 34278,77g del árbol 16 en la parcela 4 (Tabla 3).
Tabla 3. Peso seco total de cada sección diamétricas de la raíz de los 25 árboles seleccionados
|
N° de Parcela |
Arboles seleccionados |
PST raíces 0,5-2cm (g) |
PST raíces 2-5cm (g) |
PST raíces 5-10 cm (g) |
PST raíces >10 cm (g) |
PST raíz (g) |
|
1 |
17 |
72.07 |
0.00 |
62.16 |
0.00 |
134.23 |
|
12 |
897.53 |
194.61 |
0.00 |
0.00 |
1092.14 |
|
|
19 |
747.67 |
599.79 |
0.00 |
0.00 |
1347.46 |
|
|
56 |
174.90 |
0.00 |
0.00 |
0.00 |
174.90 |
|
|
2 |
77 |
108.81 |
38.59 |
0.00 |
0.00 |
147.40 |
|
35 |
31.80 |
577.92 |
378.30 |
0.00 |
988.02 |
|
|
66 |
471.66 |
648.12 |
0.00 |
798.05 |
1917.83 |
|
|
86 |
4844.15 |
5074.58 |
2884.51 |
948.90 |
13752.14 |
|
|
30 |
211.77 |
463.77 |
0.00 |
0.00 |
675.54 |
|
|
3 |
40 |
354.81 |
739.08 |
897.53 |
1111.26 |
3102.68 |
|
9 |
264.30 |
170.04 |
0.00 |
0.00 |
434.34 |
|
|
34 |
1426.92 |
1769.68 |
431.90 |
0.00 |
3628.50 |
|
|
58 |
690.03 |
2183.54 |
433.25 |
0.00 |
3306.82 |
|
|
32 |
6030.93 |
6355.85 |
3411.42 |
3462.79 |
19260.99 |
|
|
28 |
1327.28 |
986.56 |
0.00 |
0.00 |
2313.84 |
|
|
29 |
2489.89 |
575.73 |
1192.23 |
0.00 |
4257.85 |
|
|
22 |
1449.45 |
355.93 |
977.07 |
0.00 |
2782.45 |
|
|
21 |
1197.83 |
667.45 |
0.00 |
0.00 |
1865.28 |
|
|
4 |
9 |
1627.44 |
1613.87 |
0.00 |
0.00 |
3241.31 |
|
16 |
11882.75 |
6223.25 |
3930.76 |
12242.01 |
34278.77 |
|
|
20 |
7529.05 |
5961.20 |
1278.61 |
2171.86 |
16940.72 |
|
|
52 |
6759.05 |
4689.97 |
1709.94 |
2426.78 |
15585.74 |
|
|
5 |
32 |
4372.02 |
3152.52 |
1210.34 |
0.00 |
8734.88 |
|
18 |
905.57 |
201.09 |
0.00 |
0.00 |
1106.66 |
|
|
15 |
573.81 |
756.47 |
516.04 |
0.00 |
1846.32 |
Ecuaciones para estimar la biomasa de cada sección diamétricas de la raíz de Prosopis pallida “algarrobo”
Los valores del coeficiente de correlación de Pearson oscilan entre - 1 y +1, y a la vez se muestran los valores de R, R2 y R2 ajustando, obteniendo las correspondiste ecuaciones (Tabla 4).
Tabla 4. Ecuaciones para estimar biomasa según cada sección
|
Biomasa |
Ecuación de biomasa |
Coeficiente correlación |
R2 |
R |
R2 Ajustado |
p - valor |
CME |
|
0.5-2 cm |
-83,1247 + 8,39121×DAP2 |
0,81 |
66,65 |
8,16 |
65,2 |
0,000 |
3,11E+11 |
|
2-5 cm |
61,0354 + 6,09036×DAP2 |
0,82 |
68,65 |
8,28 |
67,29 |
0,000 |
1,50E+06 |
|
5-10 cm |
-150,181 + 3,30783×DAP2 |
0,85 |
72,99 |
8,54 |
71,81 |
0,000 |
3,58E+05 |
|
> 10 cm |
(-4,70054 + 0,0681477×DAP2) 2 |
0,72 |
52,33 |
7,23 |
50,26 |
0,000 |
3,74E+02 |
|
Final |
-874,247 + 23,627×DAP2 |
0,84 |
70,23 |
8,38 |
68,92 |
0,000 |
2,09E+07 |
Por último, se comprueba que la ecuación seleccionada es la ideal, ya que como se observa en la figura 4 el comportamiento de la curva de la biomasa radicular total con la biomasa estimada, en función del DAP, se aprecia que la curva se comporta de acuerdo al patrón esperado, ambas curvas se aprecian muy similares.
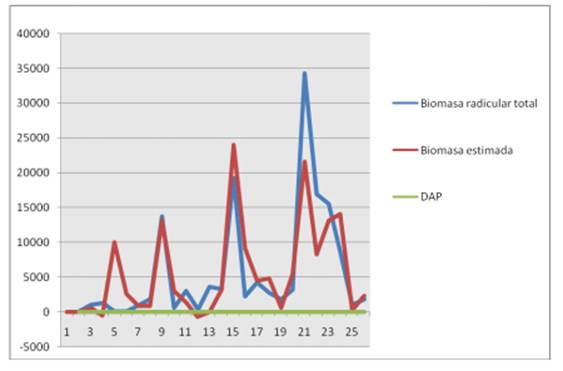
Figura 4. Relación entre la biomasa radicular total, la biomasa estimada y el DAP.
Aplicación de las ecuaciones para estimar la biomasa radicular de Prosopis pallida “algarrobo”
Ya teniendo las ecuaciones correspondientes para estimar la biomasa de las secciones diamétricas y el total, estas se aplicaron a los 359 árboles evaluados en las 6 parcelas (Tabla 5 y Figura 5).
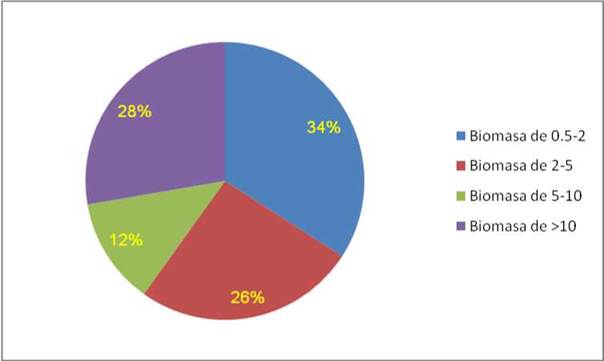
Figura 5. Distribución de la biomasa radicular estimada en los 359 árboles.
Tabla 5. Estimación de biomasa radicular de Prosopis pallida “algarrobo”
|
Ecuación de biomasa |
Biomasa estimada (g) |
|
|
Biomasa de 0.5-2 |
-83,1247 + 8,39121*DAP2 |
1,433,162,462 |
|
Biomasa de 2-5 |
61,0354 + 6,09036*DAP2 |
1,083,655,204 |
|
Biomasa de 5-10 |
-150,181 + 3,30783*DAP2 |
5,229,283,501 |
|
Biomasa de >10 |
(-4,70054 + 0,0681477*DAP2) 2 |
1,166,243,203 |
|
Biomasa Radicular Total |
-874,247 + 23,627*DAP2 |
3,806,194,081 |
El bosque natural de algarrobo de la Universidad de Piura es de 50 Ha, por lo tanto para calcular la cantidad de biomasa se extrapolo y se obtuvo una biomasa de 126,8 t/ha.
Cantidad de carbono secuestrado en cada sección de la raíz de Prosopis pallida “algarrobo”
Una vez obtenida la biomasa radicular estimada en raíz de Prosopis pallida “algarrobo” (secciones diamétricas y total) se calculó la cantidad de carbono secuestrado (Tabla 6 y Figura 6).
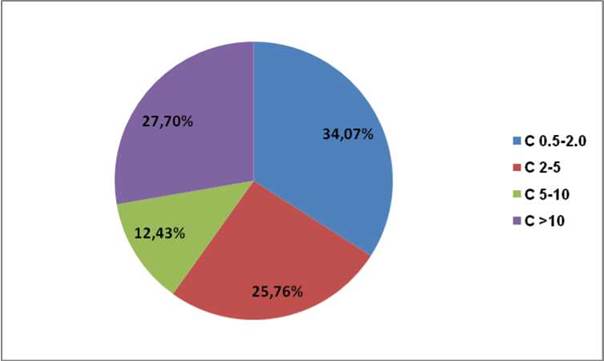
Figura 6. Distribución de la cantidad de carbono por sección diamétrica de la raíz
Tabla 6. Estimación del carbono secuestrado por cada sección diamétricas de la raíz de Prosopis pallida “algarrobo” de los 359 árboles.
|
Sección diamétrica (cm) |
Carbono almacenado (tC/ha) |
Carbono Total secuestrado |
|
0.5 - 2 |
0.717 |
2.103 |
|
2 - 5 |
0.542 |
|
|
5 - 10 |
0.261 |
|
|
>10 |
0.583 |
|
|
Biomasa total radicular |
1.903 |
|
El bosque natural de algarrobo de la Universidad de Piura es de 50ha, por lo tanto, la cantidad de carbono total secuestrado fue de 63.33 tC/ha, lo que equivale a 232,42 tCO2e
IV. DISCUSIÓN
Es sabido que el sistema radicular es decisivo para el desarrollo de las estructuras de la parte aérea del árbol, y de trascendencia en la formación del suelo (Persson, 1983), pero dado que las raíces son la “mitad oculta” de la mayoría de ecosistemas terrestres, surge la habilidad para diseñar protocolos de muestreo y esta se ve limitada por la incapacidad de observar la dinámica del sistema radicular completo de la planta, en este sentido se tiene una desventaja en el estudio de raíces, ya que la mayoría de las técnicas que estiman la biomasa radicular requieren una gran cantidad e intensidad de trabajo, y es necesario obtener una técnica por consenso debido a los pocos estudios (Chen et al., 2019), en tal sentido se aplicó un protocolo de muestreo, en donde se observó el patrón de distribución de la raíces, mediante la técnica de remoción y extracción de estos.
Se determinó que la mayor cantidad de biomasa radicular se encuentra en las secciones diamétricas de 0,5-2cmcon un 34% de la biomasa total (Figura 6). A comparación de las secciones diamétricas de 2-5cm, con 26%, 5-10cm con 12% y >10cm con 28%. La presencia de mayor biomasa en la primera sección diamétrica es debido a que esta se concentra en los primeros 40cm de profundidad. Fujita y Yanagisawa (1999) y Raich (1983) explican que el comportamiento de raíces finas, con respecto a la profundidad se caracteriza principalmente por la alta concentración de biomasa en los primeros centímetros del suelo, disminuyendo gradualmente conforme aumenta la profundidad. Esta tendencia puede ser explicada por los cambios de la compactación del suelo, el contenido de arcilla y la porosidad que afectan directamente la capacidad de absorción de humedad a lo largo del perfil del suelo, además Flores (1999) y Jensen (1994) explican que la presencia de tejidos primarios de muy baja resistencia mecánica como es el caso de las raíces finas, no pueden crecer adecuadamente bajo condiciones de compactación y altas presiones en el suelo, además por la alta compactación, existe una menor disponibilidad de aire, lo que dificulta enormemente el intercambio gaseoso de las raíces con el sustrato.
Otro de los factores que permiten que exista el comportamiento de las raíces en los primeros 40 o 50 cm de profundidad, de debe a que esta está influenciada por el sitio, la textura del suelo, y la edad de la planta (Lopez et al., 1998), asi como también las características genéticas de la especie son influyentes en la forma y distribución de los sistemas radicales, ya que pueden determinar que una especie presente raíces axomorfas o fasciculada, o bien, algunas especies presenten raíces profundas y otras superficiales (Pritchett, 1986).
La especie Prosopis pallida “algarrobo” presenta un comportamiento de raíz axomorfico, además se puede apreciar que la longitud en raíces laterales esta en 7 a 13m, en arboles con 20 a 30cm de DAP. Dalmaso et al. (1994), asegura que la longitud de las raíces supera hasta tres veces el tamaño del árbol. El suelo por su parte se encuentra formado por material de relleno en los primeros 30cm (piedras y ladrillos mezclados con arena), y luego a partir de los 40cm, contiene, arena fina limosa suelta, arena fina limosa medianamente densa, arena fina limosa densa, arcilla arenosa compacta, arcilla con arena fina compacta (IN, 2008).
En la elaboración de la ecuación alométrica, se tomaron como variables independientes el diámetro a la altura del pecho (DAP) (Gower et al., 1999, Navar, 2009) y la altura (H), de las cuales, solo la variable DAP, fue la usada por ser la más predictora (Gomez et al, 2011) y la que presento un coeficiente de correlación mayor de 80%, y la variable (H) fue descartada por presentar una correlación muy por debajo del 80%, además, para una mayor predicción de la ecuación se escogió aquella que tuvo el menor valor del cuadrado medio del error (CME). Llanos (2010), afirma que, a partir de estos estadísticos analizados, la ecuacion encontrada puede ser empleada con seguridad, ya que reflejan los resultados con bastante consistencia.
La comparación entre la biomasa total radicular y la biomasa radicular estimada (tabla 5 y figura 5), muestra que los resultados son bastante estrechos, los cuales reflejan la correcta selección de la ecuación de biomasa radicular total, el cual tuvo como parámetro definitorio el menor CME, de esta manera la ecuación queda expresada de la siguiente forma, con la variable DAP al cuadrado, BRT=-874,247 + 23,627*DAP2, arrojando que la biomasa total radicular estimada en el bosque de la Universidad de Piura, fue de 126,8t/ha.
MacDicken (1997), sugiere que también se pueden hacer estimaciones de biomasa radicular, y propone un porcentaje del 15%, en bosques de Chile, el cual considera una estimación conservadora, así como también Rodriguez et al. (2009), en México estima un 15% de biomasa en bosques de Pino-encino, Cairns et al. (1997), para la raíz/talla (R/T),para distintos lugares del mundo entrega valores entre el 20 y 30% de biomasa radicular con respecto a biomasa aérea, Grier et al. (1981), asegura que se puede hallar hasta un 30% de la biomasa aérea, estudio realizado por Laban (2012), sobre captura de carbono en el bosque natural de algarrobo en campus de la Universidad de Piura encontró 16 593 132 g de biomasa total aérea, y aplicando la relación con los 3 806 194,08g de biomasa radicular encontradas en esta investigación, nos arroja un 22,9% con respecto a la biomasa aérea, de esta manera se puede optar por aplicar de manera indirecta este valor. Cabe indicar que los árboles que fueron tomados y derribados por Laban (2012), fueron aquellos en donde se extrajeron las raíces.
Estudios en secuestro de carbono en depósitos subterráneos (raíces) son muy escasos, exigen mucho esfuerzo de tiempo y recursos en campo (Cairns et al., 1997, Clark et al., 2001). Es por ello que muchos trabajos emplean solo para parte aérea (Clark et al., 2001). O emplean modelos estadísticos (FAO, 2010) Manifiesta que la variabilidad de secuestro de carbono se atribuye, entre ellos a la región ecológica y/o climática en donde se ubican los bosques, ya que en bosques tropicales primarios varía entre 60 a 230 tC/ha y en bosques tropicales secundarios entre 25 y 190 tC/ha. Lapeyre (2003), realizo un trabajo en reservas de carbono en San Martin, bajo sistemas de bosques primarios y secundarios, y determino que el bosque primario supera ampliamente al total capturado por el bosque secundario, siendo 492 tC/ha y 235tC/ha, respectivamente. Alegre et al, (2002) estimo el secuestro de carbono en sistemas alternativos, en suelos ácidos de los trópicos húmedos del Perú y orgánicos de la sierra, fluctuaciones del carbono entre 80 tC/ha y 230 tC/ha. Los resultados obtenidos, para el secuestro de carbono en el bosque natural de algarrobo en campus de la UDEP, arrojo un 63,33 tC/ha, comparando con lo encontrado por Laban (2012), en captura de carbono aéreo, este fue de 276,50 tC/ha, el cual representa un 22,9% con respecto a la captura de carbono aérea, a partir de ello existe una relación directa de biomasa y el secuestro de carbono (Clark et al, 2001).
V. CONCLUSIONES
La biomasa radicular hallada en las 50 ha del bosque natural de algarrobo de la UDEP, fue de 126,8t/ha.
La distribución de la biomasa radicular en Prosopis pallida “algarrobo” estuvo representada de la siguiente manera: la sección diamétrica 0,5-2cm con un 34%, de 2-5cm con 26%, de 5-10 cm con 12% y >10 cm con 28%, siendo las raíces más delgadas es decir de 0,5-2cm la que presenta mayor cantidad de biomasa.
En las 50 ha del bosque natural de algarrobo del campus de la Universidad de Piura, el secuestro de carbono fue de 63,33 tC/ha.
VI. RECOMENDACIONES
Realizar otros estudios sobre biomasa radicular, en diferentes ecosistemas, por ejemplo, en bosques secos de montaña, de colina, de llanura, así como en algarrobales ribereños, para poder tener un compendio de la biomasa total que hay en el departamento.
Las ecuaciones encontradas deben ser tomadas, como referencia para bosques que tengan las características similares de esta investigación, en caso contrario se efectuaran nuevas ecuaciones.
Se debe realizar estudios en raíces menores de 0.5cm de diámetro, ya que estas también intervienen en la biomasa, como en el secuestro de carbono.
Para la extracción de raíces, es necesario contar con un grupo equipado y herramientas necesarias para realizar estos trabajos, así como un grupo capaz de trabajar bajo un gran esfuerzo físico.
VII. REFERENCIAS BIBLIOGRÁFICAS
Alegre, J., M. Arevalo, S. Risce, D. Callo y C. Palma. 2002. “Secuestramiento de carbono con sistemas alternativos en el Perú.” En I Congreso Brasilero de Sistemas Agroforestales. Ilheus (Brazil).
Adler, D. 1980. Estimación del volumen forestal y predicción del rendimiento con referencia especial a los trópicos. Predicción del rendimiento.” Roma (Italia): FAO.
Barrena V., J. Dance, S. Saenz. 1986. “Metodología para la selection de ecuaciones de volumen.” Revista Forestal del Perú 13 (2): 3- 12.
Brack, A. 1998. Ecología y Desarrollo en el Perú - Serie Cuadernos de Debate y Reflexion. Lima (Perú).
Brown S., A. J. Gillespie y A. E. Lugo. 1999. “Biomass estimation methods for tropical forests with applications to forest inventory data.” For. Sci. 35 (4): 881-902.
Brown S., A. E. Lugo. 1996. “The storage and production of organic matter in tropical forests and their role in the global carbon cycle.” Biotropica. 14 (3): 161-187 DOI: 10.2307/2388024
Cairns M., S. Brown, H. Eileen, y G. Baumgardner. 1997. “Root biomass allocation in the world's upland forest.” Oecologia, 111: 1-11.
Chen, G., S. E. Hobbie, P. B. Reich, Y. Yang, y D. Robinson. (2019). “Allometry of fine roots in forest ecosystems.” Ecology letters 22 (2): 322-331.
Clark J. S., E. C. Grimm, J., Lynch, y P. J. Mueller. 2001. “Effects of climate change on the C4 grassland/woodland boundary in the Northern Central Plains.” Ecology 82: 620¬636.
CA (Cuencas Andinas). 2004. Boletin N°1 Estrategias para el manejo integral de las cuencas en la Region Andina.
Dalmaso, A., R. Masuelli, O. Salgado. 1994. “Relación vástago - raíz durante el crecimiento en vivero de tres especies nativas del norte: Prosopis chilensis, Prosopis flexuosa y Bulnesia retama.” Multequina 3: 35-43
De Jong B., R. Tipper, y G. Montoya. 2000. “An economic analysis of the potential for carbon sequestration by forest: evidence from southern Mexico.” Ecological Economics 33 (2): 313-327. DOI: 10.1016/S0921-8009(99)00162-7
FAO (Organización de las Naciones Unidas para la Alimentación y la Agricultura). 2001. Situation de los bosques del mundo. Roma (Italia): FAO.
FAO (Organización de las Naciones Unidas para la Alimentación y la Agricultura). 2010. Inventario Forestal Nacional Nicaragua. Rome (Italia): FAO.
Flores, E. 1999. La planta, estructura y funcion. Cartago (Colombia): C.R. LUR.
Fujita N., y N. Yanagisawa. 1999. “Different distribution patterns of woody species on a slope in relation to vertical root distribution and dynamics of soil moisture profiles.” Ecological Research.14: 165-177.
GRP (Gobierno Regional de Piura). 2010. “Memoria Descriptiva del Mapa de ocupación del Territorio y Uso Actual del Suelo. Zonificación Ecológica Económica de la Región Piura.” Pirua (Perú)
Gomez J., J. Etchevers, A. Monterrosos, J. Campo, y Tinoco. 2011. “Ecuaciones alometricas para estimar biomasa y carbono en Quercus magnoliaefolia.” Revista Chapingo Serie Ciencias Forestales y del Ambiente 17 (2): 261-272, 2011
Gower S. T., C. J. Kucharik, J. M. Norman. 1999. “Direct and indirect estimation of leaf area index, F (APAR), and net primary production ofterrestrial ecosystems.” Remote Sensing Environment 70: 29-51.
Grier C., K. A. Vogt, M. R. Keyes, y R. L. Edmonds. 1981. “Biomass distribution and above- and below-ground production in young and mature Abies amabilis ecosystems of the Washington Cascades.” Canadian Journal of Forest Research 11:155-302.
Guerra, J. 2001. Contenido de carbono y funciones de biomasa en especies nativas y exoticas. Informe Técnico. Valdivia (Chile).
Herrera, S. 2002. Estimation de carbono almacenado en el tipo forestal Roble - Rauli, Coigue (Nothofagus obliqua), para determinar los beneficios ambientales de someterlo a sumideros. Informe Técnico. Santiago de Chile (Chile).
Holdridge, L. R. 1967. Life zone ecology. San José (Costa Rica); Tropical Science Center.
IN (Ingeniería del Norte). 2008. Estudio de mecánica de suelos Piura. Informe Técnico. Piura (Perú)
Jensen, W. 1994. Botánica. Ciudad de México (México): Mc Graw-Hill
MacDicken, K. 1997. “A guide to Monitoring carbon storage in forestry and agroforestry Projects.” Winrock international Institute for Agricultural Development.
Navar J., T. J. Synnott. 2009. “Soil erosion and land use in northeastern Mexico.” Terra Latinoamericana, 18 (3):247-253.
La Torre Cuadros, M. y R. Linares. 2008. “Mapas y clasificacion de vegetation en ecosistemas estacionales: un analisis cuantitativo de los bosques secos de Piura.” Revista Peruana de Biología 15 (1): 31-42.
Laban, C. 2012. Captura de carbono en el bosque natural de algarrobo del campus de la Universidad de Piura. Tesis de Grado. Universidad Nacional de Piura. Piura (Perú)
Lapeyre, T. 2003. Determinación de las reservas de carbono de la biomasa aérea, en diferentes sistemas de uso de tierra en San Martin. Tesis de Maestría. Universidad Nacional Agraria la Molina. Lima (Perú)
Llanos, M. 2010. Determinación de biomasa aérea total de algarrobo Prosopis pallida (h&b. ex. Willd.) h. b. k. Var. pallida Ferreira en los bosques secos de la comunidad campesina Jose Ignacio Pasapera del departamento de Piura. Tesis de Grado. Universidad Nacional Agraria la Molina. Lima (Perú)
Lopez B., S. Sabate, y C. Gracia. 1998. “Fine roots dynamics in a Mediterranean forest: effects of drought and stem density.” Tree Physiology 18 (8-9): 601-606. DOI: 10.1093/treephys/18.8-9.601
Persson H. D. 1983. “The distribution and productivity of fine roots in boreal forest.” Plant and Soil 71: 87-101.
Philip, M. 1994. Measuring Trees and Forests. Londres (Reino Unido): Oxon
Pritchett, W. 1986. Suelos forestales: propiedades, conservation y mejoramiento. Ciudad de México (México): LIMUSA.
Raich J. 1983. “Fine roots regrow rapidly after forest felling.” Biotropica.15: 177-184.
Rodríguez L., P. Jimenez, y C. Aguirre. 2009. “Estimation de carbono almacenado en el bosque de Pino- Encino en la reserva de la biosfera el Cielo, Tamaulipas, Mexico.” Ra. Ximhai 5 (3): 317-327.
Salimon C.I y I.F. Brown. “2000. Secondary forests in wester Amazonia: significant sinks for carbon released from deforestation.” Interciencia 25: 198-202.
Schlegel, B. 2001. “Estimation de la biomasa y carbono en bosques del tipoforestal siempreverde.” En VI Simposio International Medición y Monitoreo de la captura de carbono. Santiago de Chile (Chile)
Schlegel, B., J. Gayoso, y J. Guerra. 2000 Metodos de medicion de biomasa forestal. Medicion de la capacidad de captura de carbono en bosques de Chile y promocion en el mercado mundial. http://www.capturacarbono.co.cl/textos/manincar.pdf (Consultado el 22 de agosto del 2010).
Trumper K, C. Ravilious, y B. Dickson. 2008. “Carbon in Drylands: Desertification, Climate Change and Carbon Finance.” Informe Técnica. Estambul (Turquía).
Vidal A., J. Benitez, J. Rodriguez, R. Carlos, y H. Gra. 2003. “Estimación de la biomasa de copa para árboles en pie de Pinus caribaea var. Caribaea la E.F.I. La Palma de la provincia de Pinar del Rio, Cuba.” Quebracho - Revista de Ciencias Forestales 11: 60-66.